Understanding Overlap: in 1 or 2 dimensions

tl;dr

The answer is on stackoverflow:

if (RectA.Left < RectB.Right && RectA.Right > RectB.Left &&
    RectA.Top > RectB.Bottom && RectA.Bottom < RectB.Top)

which is correct but not especially obvious.

A LOT of people think the stackoverflow answer is wrong and try to “fix” it 🤣

Step by step: in one dimension

Let’s simplify the problem:

• let’s focus only on one dimension – the x axis
• let’s use rectangles – just ignore their heights
  (it’s easier to visualize than line segments)

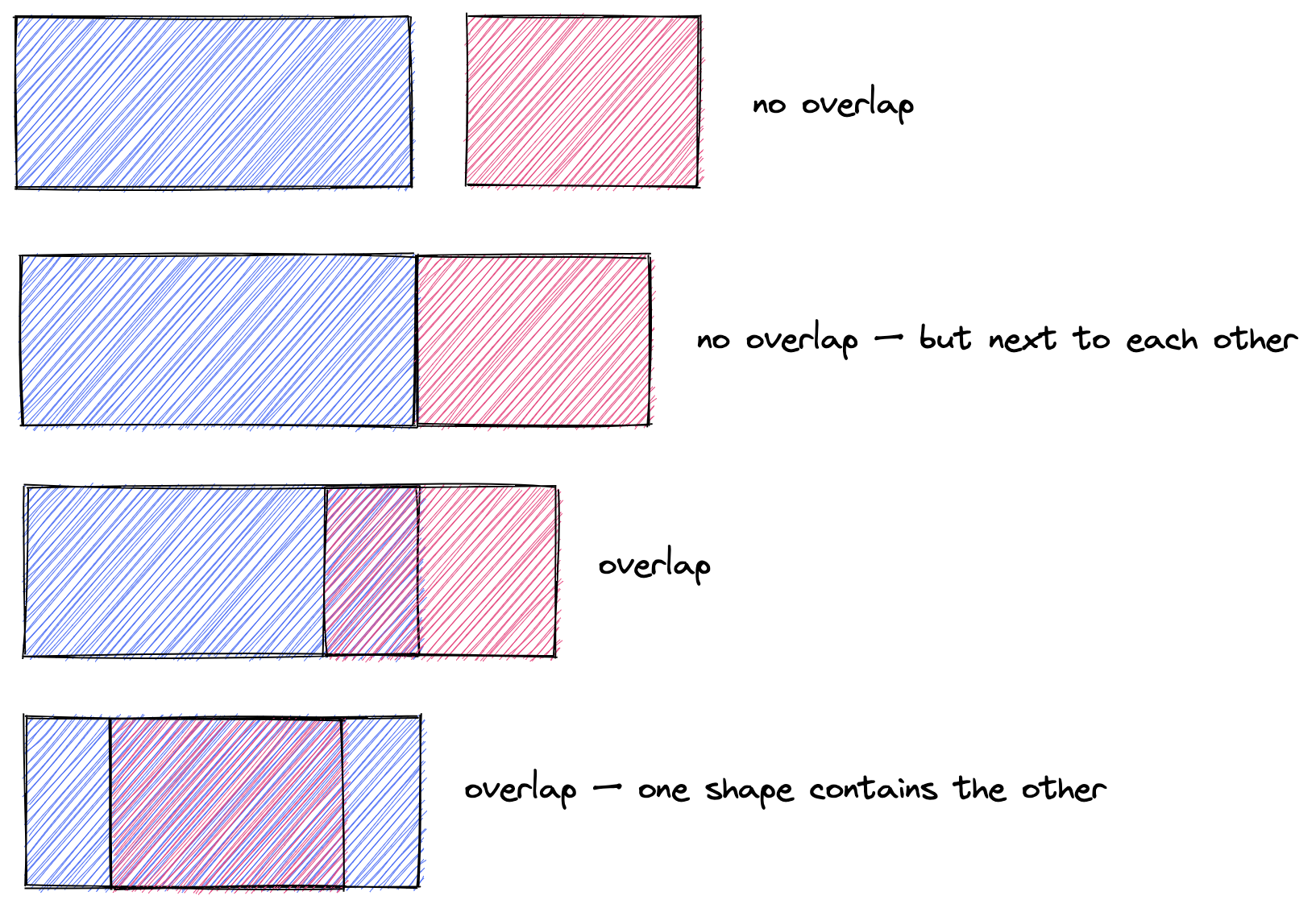
How can 2 rectangles overlap in one dimension?

There seems to be a lot of cases 🤔

• left of B could be inside A
• (or) right of B could be inside A

But what about this?

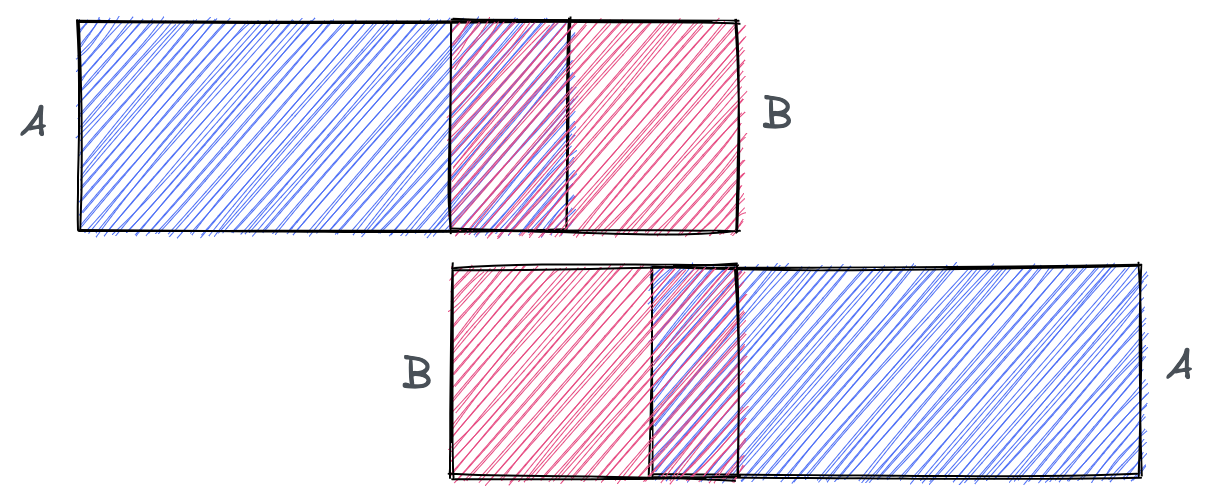
Both sides of B are inside A. But neither of A’s sides are inside B. We need symmetry…

What are we left with?

• left of B could be inside A
• (or) right of B could be inside A
• (or) left of A could be inside B
• (or) right of A could be inside B

Simple? Did we cover all the cases? (no! read until the end)

Personally, that’s when I turned to stackoverflow.

A different perspective

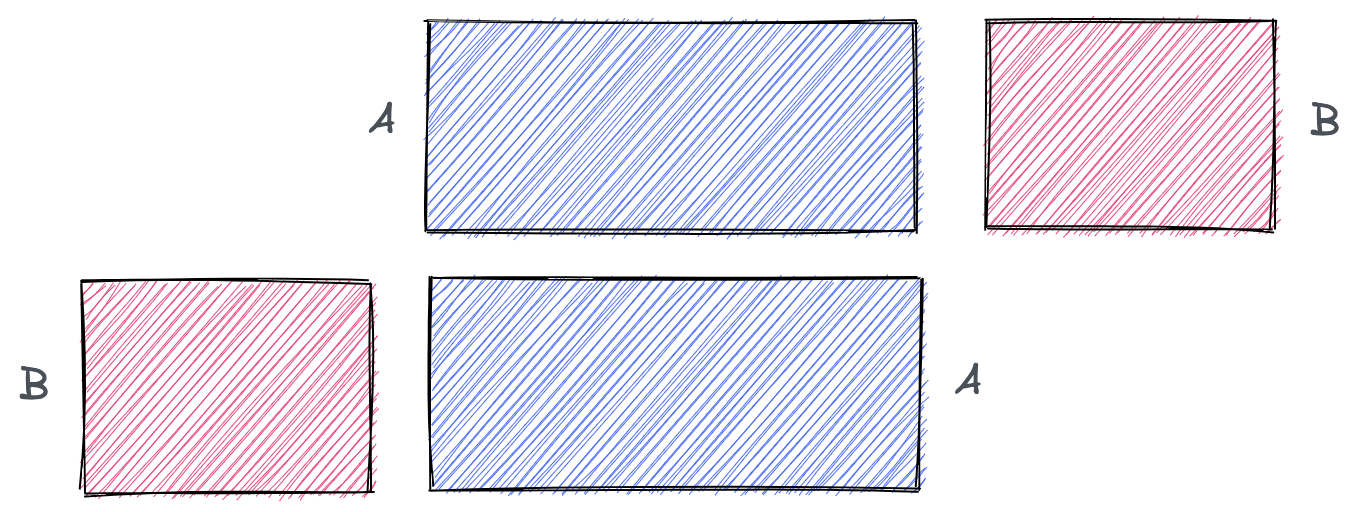
If overlap is hard to pin down, let’s try to define the opposite: what does it look like when rectangles do NOT overlap?

in English:

• A is to the left of B
• (or) A is to the right of B

let’s turn this to pseudo-code:

no_overlap = a.right < b.left || a.left > b.right
// in other words, overlap is the inverse
overlap = !(a.right < b.left || a.left > b.right)

De Morgan’s Laws say that:

• not (A or B) = (not A) and (not B)
• not (A and B) = (not A) or (not B)

// unchanged, from above
overlap = !(a.right < b.left || a.left > b.right)

// applying De Morgan: conditions inverted, || becomes &&
overlap = !(a.right < b.left) && !(a.left > b.right)

// flipping > and < comparisons
overlap = a.right > b.left && a.left < b.right

// reorganizing order of conditions (to match stackoverflow...)
overlap = a.left < b.right && a.right > b.left

Looping back to the beginning, check the first line of answer:

if (RectA.Left < RectB.Right && RectA.Right > RectB.Left &&
    RectA.Top > RectB.Bottom && RectA.Bottom < RectB.Top)

What about 2d?

The same “to-the-left-of” or “to-the-right-of” cases apply. You also need to consider “above” and “below” cases.

(top and bottom are relative to … the direction of your y-axis) 😬

// unchanged, from above
overlap = !(a.right < b.left || a.left > b.right ||
            a.bottom > b.top || a.top < b.bottom)

// applying De Morgan: conditions inverted, || becomes &&
overlap = !(a.right < b.left) && !(a.left > b.right) &&
          !(a.bottom > b.top) && !(a.top < b.bottom)

// flipping > and < comparison
overlap = a.right > b.left && a.left < b.right &&
          a.bottom < b.top && a.top > b.bottom

// reorganizing order of conditions (to match stackoverflow...)
overlap = a.left < b.right && a.right > b.left &&
          a.top > b.bottom && a.bottom < b.top

Back to this:

if (RectA.Left < RectB.Right && RectA.Right > RectB.Left &&
    RectA.Top > RectB.Bottom && RectA.Bottom < RectB.Top)

Edge Case

What case did we miss earlier?

• 2 rectangles
• same dimensions
• exactly on top of each other

In that case, neither rectangles is inside the other… but the stackoverflow solution works for all cases 😄

Discussion

Depending on your situation, the width of your rectangle boundary (1 pixel, or whatever units) might make a difference: consider changing </> to <=/>= if needed.

If you’re still not convinced, try this interactive tool.