Statistics: How Many Would You Check?

Russian Translation, thanks to Vlad.
Ukrainian Translation, thanks to Sandi.
Estonian Translation, thanks to Johanne.
Spanish Translation, thanks to Laura.
French Translation, thanks to Jean-Etienne.
Urdu Translation, thanks to Samuel.
Sindhi Translation, thanks to Samuel.

Imagine this situation:

You just performed a batch update on millions of users in your database. There were no error messages and you are confident that everything went well. But it wouldn’t hurt to check…

How many users would you have to check to feel confident that everything worked for at least 95% of users?

Here are some thoughts:

• if you don’t check, you don’t know: confidence is 0%. After all, maybe your batch update didn’t work at all, but there were no error messages.
• if you check ALL, you know the answer: confidence is 100%. But that might be a lot of work…
• if you check some users, maybe 10, and the update worked … you can start to feel good. How confident can you be?

I don’t think the answer is obvious. I had to take some time to think about it.

A detour: average rating

I remembered reading How Not To Sort By Average Rating, and I thought I could apply the same logic to this problem.

If you only have one review, and it’s positive, is that 100%? Intuitively, we know that it’s not: it’s just one person’s opinion. As more and more people give positive reviews, we can start feeling better about the accuracy of the score.

The quote from the article is:

Given the ratings I have, there is a 95% chance that the “real” fraction of positive ratings is at least what?

We can use the lower bound of the Wilson confidence interval.

In practice, with R

The binom.wilson function, from the binom package, can be used like this:

> binom.wilson(18, 20)
    method  x  n mean     lower     upper
  1 wilson 18 20  0.9 0.6989664 0.9721335

In other words, if we sampled 18 positives and 2 negatives (18/20), the “real” fraction probably falls between 0.699 and 0.972 (mean: 0.9).

For our example, we could invoke it with 100% success:

> binom.wilson(10, 10)
    method  x  n mean     lower upper
  1 wilson 10 10    1 0.7224672     1

The upper bound isn’t interesting: we’re not interested in the best case scenario. But if you check 10 and they are all successful, you can feel confident that it worked for (lower bound) 72.2% of users.

If we keep checking, and we keep finding successes, we can feel more and more certain about “true” success:

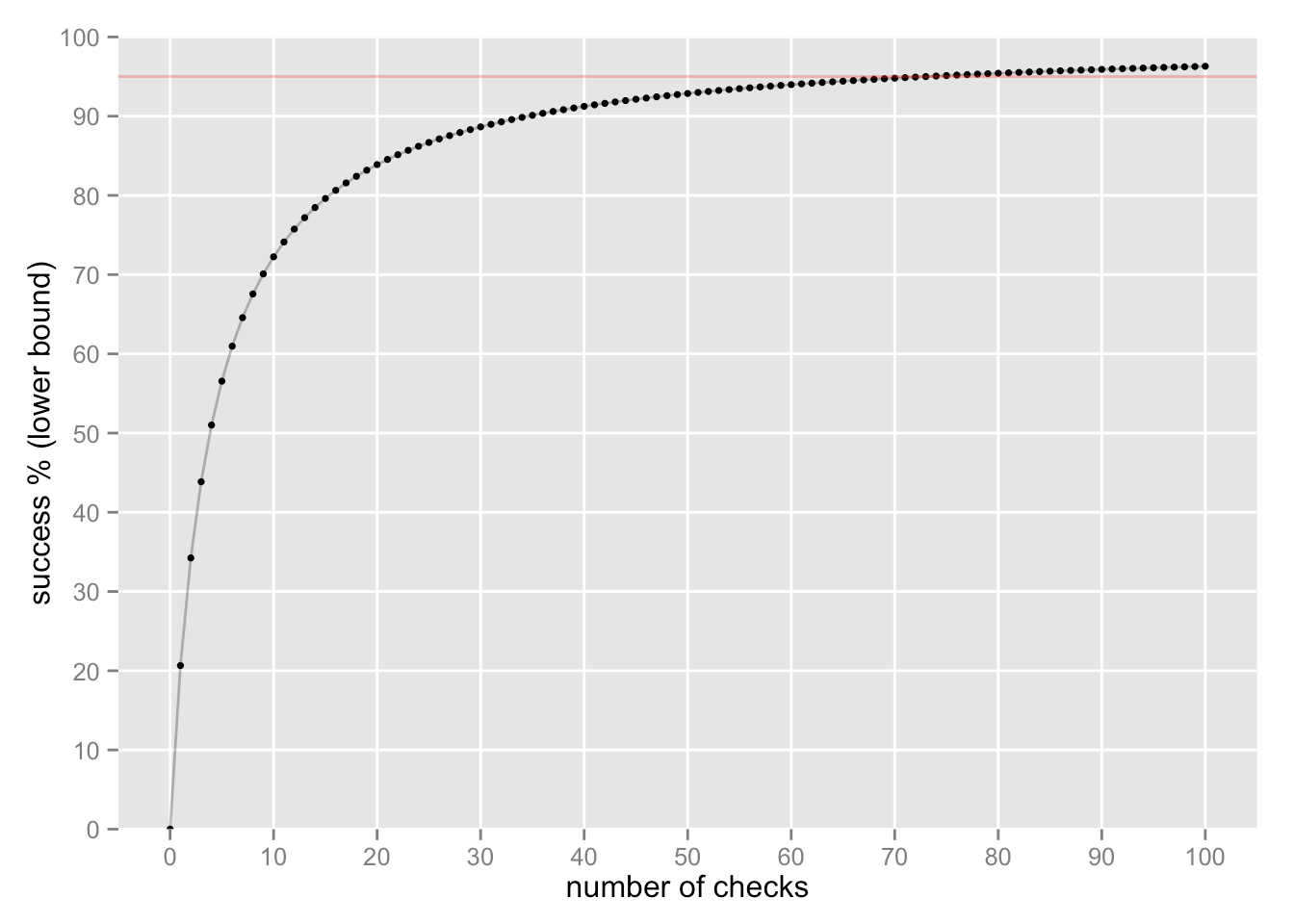
It takes 73 checks to reach a lower bound of 95% of “true” success (the red line).

Analysis

Here is the analysis as a RMarkdown document and the resulting output html document.