How to Cut a Rectangle into 3, without a Ruler
Background
It wasn’t my first time standing over a lasagna pan, trying to eyeball how to cut it into 6 equal portions.
Cutting anything in 2 seems relatively easy to estimate. And, in the worst case, you can fall back on I cut, you choose.
What about cutting in 3? Eyeball it? Is there a better way?
- no rulers available
- but something like a square to make straight lines and 90° angles
- as precise as possible, exact if possible
Short version
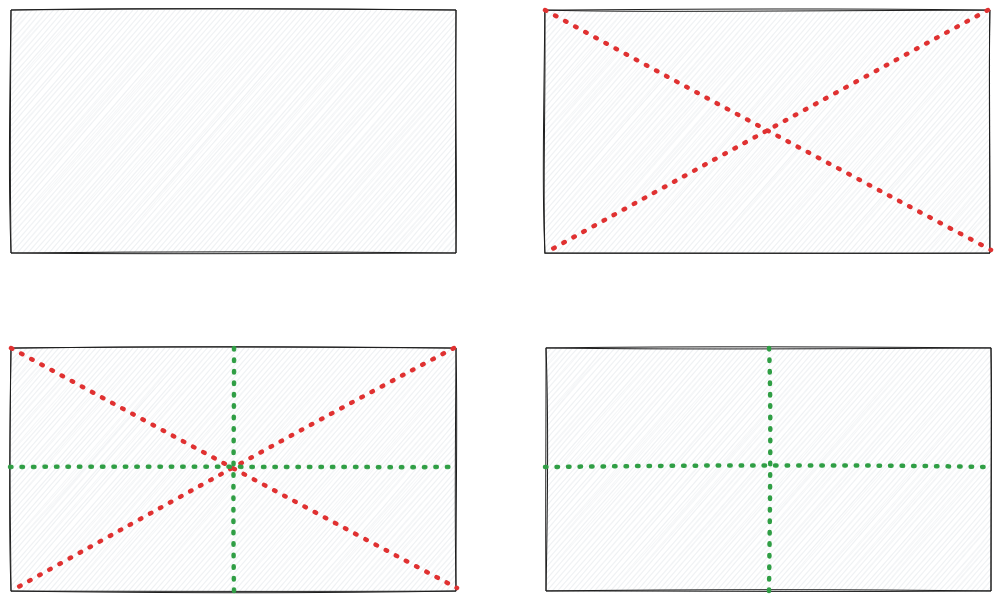
Warm up: how to divide in 2
- red: diagonals to opposite corners, to find the middle
- green: perpendicular lines to the edges, through the middle
- only green lines matter
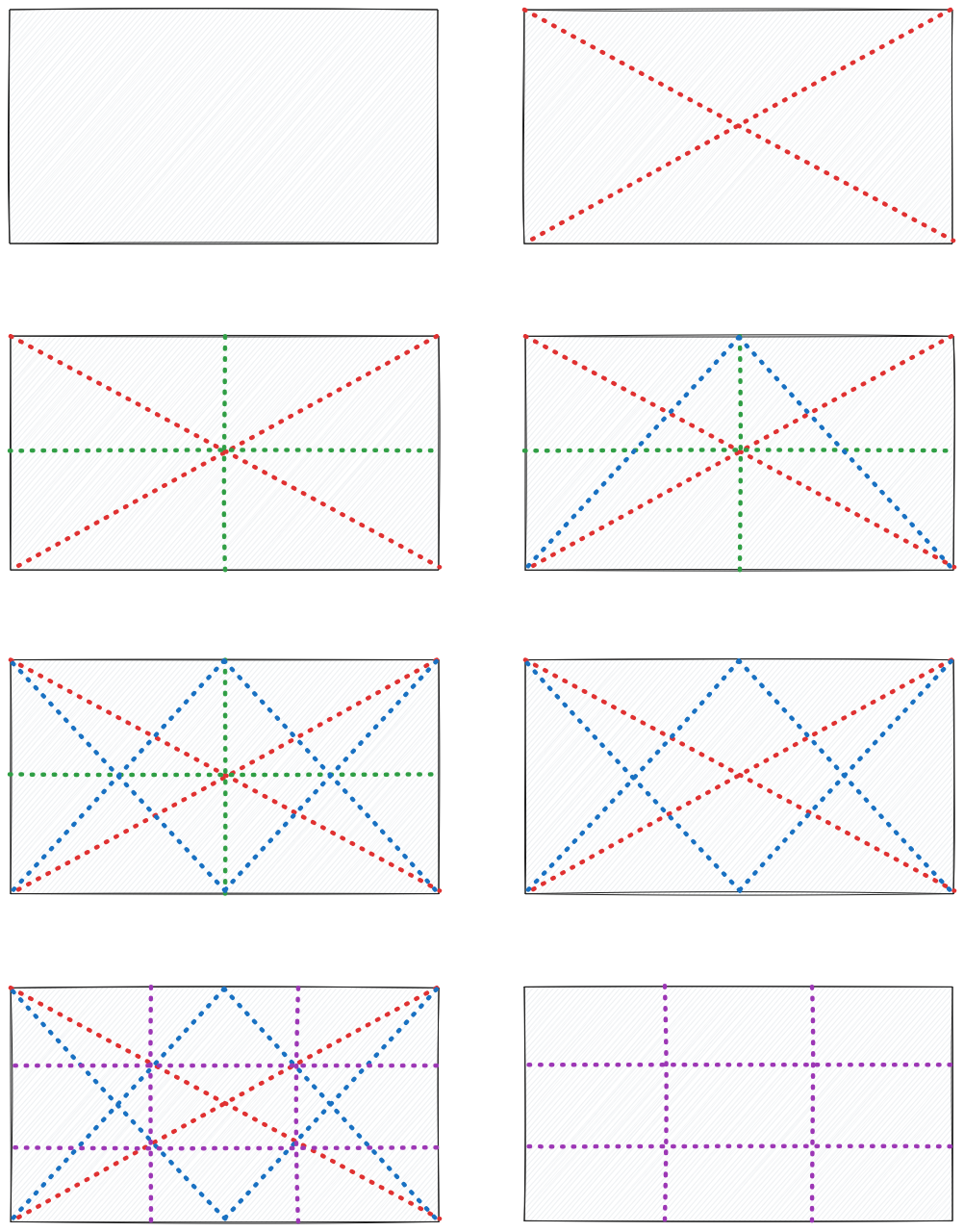
How to divide in 3
This isn’t “obvious”; take some time with it. I discuss my “shortcuts” in the next section.
- same steps to red and green lines
- blue: from middle to opposite corners (here shown in 2 steps)
- green: forget the green lines, we won’t need those anymore
- purple: through red-blue intersections, horizontally and vertically
- only purple lines matter
What I actually do…
When, knife in hand, I try to cut in 3, I take some liberties 😆
- I “imagine” the middle point of the top edge, by eye…
- I imagine the red and blue line, by eye…
- I mark the intersection
- I cut down horizontally/vertically through that point, depending on what I need
But … what about the rest?!
The right side is 2/3 and I can divide that in halves by eyeball. (it’s the same situation on the way down)
What’s the point of this?
Mostly, I was curious about finding an exact method.
This definitely works, but I couldn’t find a great explanation. I tried to find a geometrical proof but I was stumped. In the end, I solved for the intersection using the slopes of the lines.
- if W is the width of the rectangle
- if H is the height of the rectangle
- if the bottom-left side of rectangle is (0,0)
- red line:
y = -H/W x + H - blue line:
y = 2H/W x - solved in Wolfram Alpha
If you need to be precise, don’t skip any steps – but you decide how exacting your in-the-moment requirements are.
Bonus
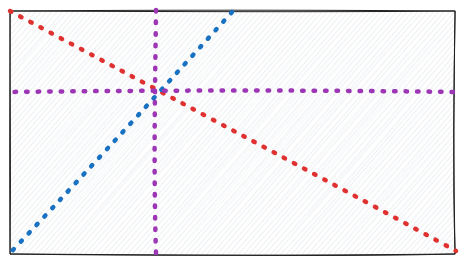
This technique also works in perspective (!)
Do you recognize the line work?